前回は視覚の話が出ましたので、関連して色の話です。
人間が見ている映像は反射した光が人の眼を通して見えています。景色には色がついています。元々太陽光は人には無色(白色)に見えていますが、光が物に反射すると、固有の波長の光が吸収されて、吸収されなかった波長の光が人の眼に入ります。偏った波長の分布を持った光が波長特有の色として見えるのです。
人の眼が色として感じることが出来る波長は380~780ナノメートルといわれています。いわゆる可視光です。太陽光が色として偏りのある波長分布になるのは反射するときだけではありません。雨上がりに見える虹も太陽光からの光が波長により色分解されて発色しているのです。光は電磁波の一種でまっすぐに進む性質を持ちますが、性質の異なる物質に進むとき、例えば空気から水、空気からガラスへといった場合、斜めに入った光は角度を変えて進む性質があります。この現象を屈折と呼ばれていて、波長の短い青~紫の波長ほど大きく角度を変えて進む性質があります。
プリズムを通過した光が虹色に見えるのはこうした光の性質によるものなのです。
 |
| プリズムによる光の分光 |
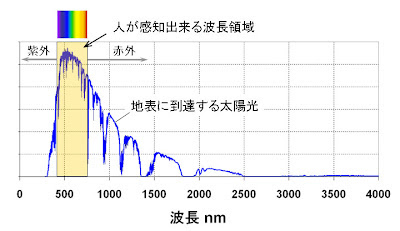
七色の虹と言われるように虹は7色で表現されますが、本当に7色しか色がないのかというとそうではなくて赤、橙、黄、緑、青、藍、紫が連続的に変化して無数の色があるのです。人間は虹の色で表されている波長の光を視神経が感じているわけですが、太陽はもっと広い波長領域の光(電磁波)を放っているのです。赤より波長の長い部分を赤外線、紫より波長の短い光を紫外線と呼んでいます。太陽からは280nm~3,600nmの広い波長域を持った電磁波が放出されています。赤色に見える光の波長は610~780ナノメートル(nm)紫に見える波長は380~430nmですから、人は太陽光のほんの一部の波長領域しか感じることが出来ないのです。
しかし太陽光のスペクトル分析を行うと人が感じることが出来る500nm付近にピークがあり人間は効率的に太陽光を活用した動物であると言うことも出来るのです。